Functional Analysis

Forward-backward parabolic equations

Summer Term 2015
Selected Topics in PDE and Mathematical Models (V5B4)
Dr. M. Helmers

 

Lectures Friday 12–14 in room SR0.006

Synopsis

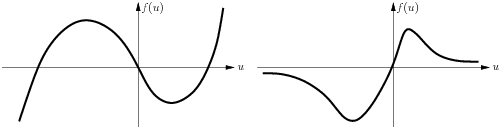
The nonlinear diffusion equation \[ \partial_t u = \Delta f(u), \tag{1} \] where \(f\) is a function with increasing as well as decreasing branches as in the figure below, appears in different applications such as edge detection in digital images, models for population dynamics, or phase separation problems with supercooling and superheating. However, if the initial data for \(u\) lie in the decreasing branch(es) of \(f\), equation (1) is ill-posed within the classic framework of PDEs.

 

Nevertheless, solutions to (1) can be obtained by different regularization procedures. Moreover, these solutions often display complex dynamical features such as phase transitions, hysteresis, microstructure and coarsening, which put a comprehensive existence theory for arbitrary right hand side and initial data far out of reach.

 

Two examples of a right hand side \(f\). On the left, the decreasing branch is enclosed by two increasing branches, so (1) is parabolic for small and large values of u and backwards parabolic in between. On the right, the equation is parabolic for small \(|u|\) and backwards parabolic for large \(|u|\).

Detailed programme

  1. Introduction:
    • Gradient flow structure and some dynamic features of the forward-backward equation; different regularizations
  2. The viscous approximation:
    • Solutions to the approximate equation, boundedness and energy estimates
    • Young-measure solutions to the limit equation
    • Entropy inequality
    • Two-phase problem
    • Long-time behaviour
  3. The Cahn-Hilliard equation (in 1D)
    • Setup of approximate solutions and limit
    • Convergence
    • Two-phase problem

Examination

The course will be completed by an oral exam on 30. and 31.07.15.

Literature

Section 2 on the viscous approximation is based on the following papers.

  • A. Novick-Cohen, B. Pego. Stable patterns in a viscous diffusion equation. Trans. Amer. Math. Soc. 324(1), 331–351, 1991.
  • P. I. Plotnikov. Passing to the limit with respect to viscosity in an equation with variable parabolicity direction. Differential Equations 30(4), 614–622, 1994.
  • L. C. Evans, M. Portilheiro. Irreversibility and hysteresis for a forward-backward diffusion equation. Math. Models Methods Appl. Sci. 14(11), 1599–1620, 2004.
  • F. Smarrazzo, A. Tesei. Long-time behavior of solutions to a class of forward-backward parabolic equations. SIAM J. Math. Anal. 42(3), 1046–1093, 2010.

Section 3 on the Cahn-Hilliard equation is based on

  • G. Bellettini, L. Bertini, M. Mariani, M. Novaga. Convergence of the one-dimensional Cahn-Hilliard equation. SIAM J. Math. Anal. 44(5), 3458–3480, 2012.

Some material on Young-measures can be found in Section 3 of

  • S. Müller. Variational models for microstructure and phase transitions. Lecture Notes in Math. 1713, 85–210, Springer 1999.

Links